|
9
The Rabi model is a semi-classical model. This means that we use a classical
representation of the field
| |
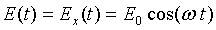 |
(3.1) |
For the atom we use a quantized description, so the atom has two states; the ground state and the
excited state
| |
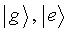 |
(3.2) |
The atom-field interaction is described by the interaction Hamiltonian
| |
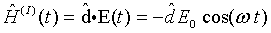 |
(3.3) |
where
| |
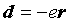 |
(3.4) |
The interaction Hamiltonian can be seen as the energy flow between the atom and the field.
The total Hamiltonian of a quantum mechanical atom-field interacting system is
| |
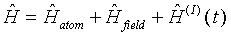 |
(3.5) |
The free-atom Hamiltonian is
| |
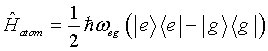 |
(3.6) |
We choose the energy of the ground state of the atom to be zero, so the free-atom Hamiltonian
becomes
| |
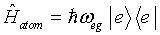 |
(3.7) |
Because we do not use a quantum field, there is no free-field Hamiltonian. So the total Hamiltonian
becomes
| |
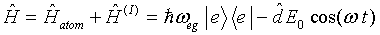 |
(3.8) |
The state vector of the system is
| |
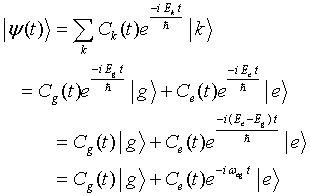 |
(3.9) |
Substituting this expansion in the time-dependent Schrödinger equation
| |
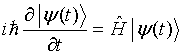 |
(3.10) |
gives
| |
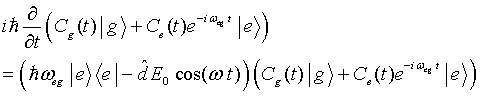 |
(3.11) |
leads to the set of coupled first-order differential equations for the amplitudes
| |
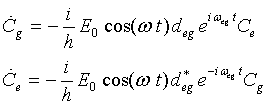 |
(3.12) |
As initial conditions we assume that all the population is in the ground state at t=0, so near t=0
| |
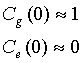 |
(3.13) |
After we have expanded cos(ωt) in exponentials and apply the Rotating Wave Approximation (RWA,
retain only the terms oscillating with ωeg-ω) we obtain
| |
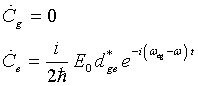 |
(3.14) |
At this point we introduce the detuning Δ
| |
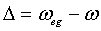 |
(3.15) |
By integrating the differential equation 3.14, the solution is
| |
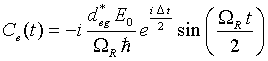 |
(3.16) |
where
| |
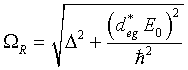 |
(3.17) |
is the Rabi frequency. The probability that the atom is in its excited state is
| |
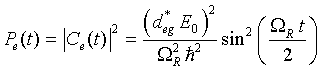 |
(3.18) |
Equation 3.18 is plotted in figure 9 for various values of the detuning Δ. The smaller the detuning the
larger the probability of finding the atom in its excited state. If you want to see Rabi oscillations, you need an
atom in its excited state (see figure 8). For the case of exact resonance, Δ = 0,
we have at the time
| |
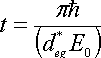 |
(3.63) |
all the atomic population has been transferred to the excited state. This is the ideal situation for Rabi oscillations.
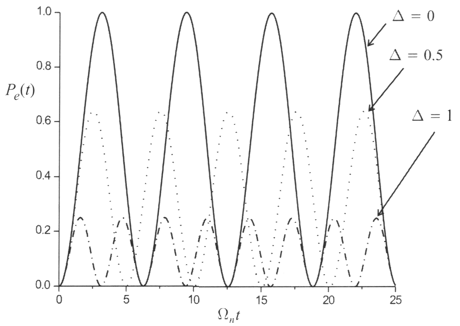
Figure 9: Plots of P e(t) versus t for various detuning Δ 9
|
Click here to learn more about the Jaynes-Cummings model.
|






